.
BREVE RESEÑA HISTÓRICA
Las cónicas fueron descubiertas accidentalmente por Menecmo (350 A.C.) pero fue Apolonio de Pergamo (262-190 A.C.) el primero en estudiar detalladamente las curvas cónicas desc que las cónicas se podían clasificar en tres tipos a los que dio el nombre de: elipses, hipérbolas y parábolas; además demostró que las curvas cónicas tienen muchas propiedades interesantes como las de reflexión.
Se dice que Arquímedes (287-212 A.C.) defendió Siracusa incendiando naves romanas utilizando las propiedades de los espejos parabólicos, más tarde René Descartes (1596-1650) tuvo la genial idea de relacionar las gráficas con las ecuaciones a este método ahora le llamamos Geometría Analítica.
Johannes Kepler (1570-1630) demuestra que la trayectoria de los planetas alrededor del sol son elipses.
hoy en día cuando estudiamos estos contenidos nos diera la impresión que son entes abstractos que no tienen ninguna relación con la vida real, sin embargo En nuestro entorno existen muchas aplicaciones de las mismas, las cuales utilizamos sin siquiera darnos cuenta, que están con nosotros ayudándonos en nuestro diario vivir.
Las figuras que se van a estudiar, reciben el nombre genérico de cónicas, ya que todas ellas se obtienen de la intercepción de un plano con una superficie cónica.
Superficie Cónica: recibe este nombre la superficie engendrada por una línea recta que gira alrededor de un eje manteniendo un punto fijo sobre dicho eje:
Cónica: se denomina simplemente Cónica a la curva obtenida al cortar esa superficie cónica con un plano las diferentes posiciones de dicho plano nos determinan distintas curvas: Circunferencia, Elipse, Hipérbola y Parábola.
Si β > a entonces el plano corta a todas las generatrices de la superficie cónica y, por tanto, se obtiene una curva cerrada. Si β ≤ a se obtiene una curva abierta.
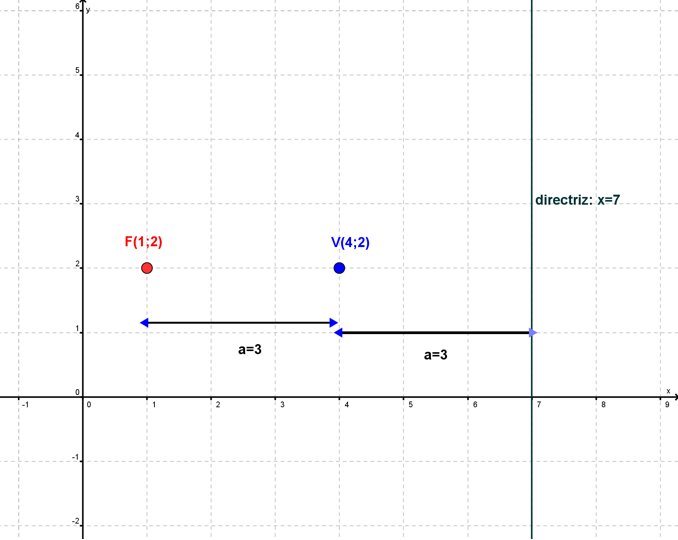
Parábola.- es la curva que se observa al cortar la superficie conica con un plano paralelo a la generatriz
Elipse.- es la curva que se observa al cortar un cono con un plano oblicuo respecto al eje.
Hipérbola.- Es la curva que se genera al cortar una superficie cónica con un plano paralelo a la base, pero que no pasa por el vértice de la superficie cónica.
CÓNICAS DEGENERADAS
Las cónicas propiamente dichas son las que ya se han descrito: circunferencia, elipse, hipérbola y parábola. Sin embargo, desde un punto de vista matemático conviene a veces considerar como cónicas las figuras que se obtienen al cortar la superficie cónica mediante planos que pasan por su vértice. A estas figuras se les llama cónicas degeneradas. Según esto, una recta, un par de rectas, o incluso un punto, serían cónicas degeneradas.
EXPRESIÓN ANALÍTICA DE LAS CÓNICAS
Desde un punto de vista analítico se puede definir cónica como la curva que responde a una ecuación del tipo:
Ax2 + By2 + Cxy + Dx + Ey + F = 0
Los valores que toman A, B, C, D, E y F, determinan el tipo de la cónica y su posición en el plano. Permitiendo que dichos coeficientes tomen valores cualesquiera, además de los cuatro tipos de cónicas, se obtienen cónicas degeneradas e incluso cónicas imaginarias.
SECCIONES CÓNICAS
CÓNICAS DEGENERADAS
EXCENTRICIDAD DE LAS CÓNICAS